01 パスとは何か
|
1:パスのについての私見 さて、私のイラストの描画手順を語る上で、Photoshopのパス機能は、絶対に避けて通れないものです。 今回の講座のメインディッシュに私が考えている機能ですが、意外にこのパス、講座で機能から詳細に説明しているサイトは少ないようです。 このサイトのすべての描画手順を見てもらえれば、製作者の意図としては非常に喜ばしいことですが、パスの機能を知りたくてこの講座を閲覧しているということでも私は十分だと思っています。 パスに関して、少なくとも私の絵に関してはそれくらい重要なものと位置付けています。 そしてパスについて全く知識が無くても描けるようになれるようにと考えて、この講座を開いています。 この「No.04」の章は、一旦イラストから離れて、パスの基礎的な機能について説明しています。ですから、「パスの機能は理解しているから絵の描画手順を見たい」という方は、この章は飛ばして「No.05」へ移ってください。 2:パスの原理 では、パスとはどのような原理で描かれているのでしょうか。 先ずはそこから入っていきたいと思います。 パスにはアンカーポイントと呼ばれるポイントを指定して、そのポイントからでる方向ベクトル情報(方向線とも呼ぶ)をもとに、ラインを生成します。 パスにはラインそのものの情報は含まれず、このアンカーポイントと方向ベクトル情報で、その間を埋めるラインを算出して描画しています 完全に計算式に乗っ取った描画ですから、二つの点の間は、非常にスムーズなラインを生成してくれるわけです。 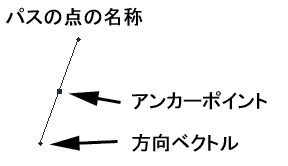 図1:各部の名称 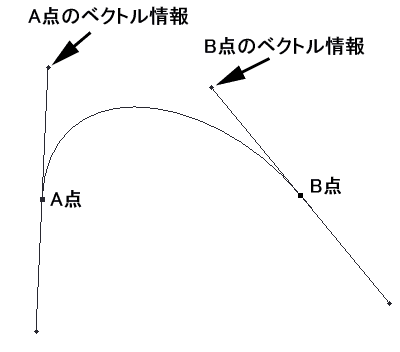 図2:A点とB点を結んだパスの例 さてここに、任意のA点とB点をベクトル情報つきのパスで作成してみた例を示してみました。 このA点とB点をどのようにパスのラインで描画しているか、分かりますか? すこし数学的な知識が必要になりますが、この部分の原理を分かっておくと、ラインを描画するのがかなり直感的に行えるようになる(筈)ですので、一応目を通しておくことをお勧めします。 3:パスの数学的見解 (上級編) Photoshopにおける「パス」は、一般的にベジェ曲線と呼ばれるライン描画手法を用いた計算式を採用しています。 尚、ベジェとは、このライン手法を最初に考案したフランス人(Bezier)の名からきています。 ここでは各点を分かりやすくするために、アンカーポイントと方向ベクトル情報を「α β γ δ」で記載してみます。 図3を参照してください。 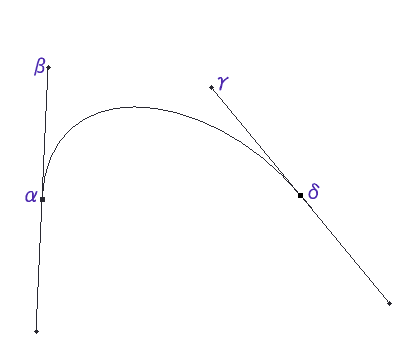 図3:各点を置き換えた例 それぞれの点は位置ベクトルと呼ばれ、点には方向性がありません。 また計算式によって求められるのは「点の集合」であって、それ単体はベクトルではありません。これをスカラーと呼びます。この場合におけるベクトルライン rの方程式は以下のようになります。 この式は t=0 のときα、t=1のときβとなります。tが0から1に変化するとともに、r(t)の値は α>β>γ>δ の順に移っていきます。 計算式では難しいので、これを図式で表現してみましょう。 先ず、ベクトルのラインはその特性上、4点が凸多角形の場合、その多角形内に必ず入ります。今回の点、α、β、γ、δは凸多角形ですから、この法則に入るというわけです。 また、ベクトルは αの点から必ず出発し、δの点で必ず終了します。この場合の点を簡単に表現してみましょう。 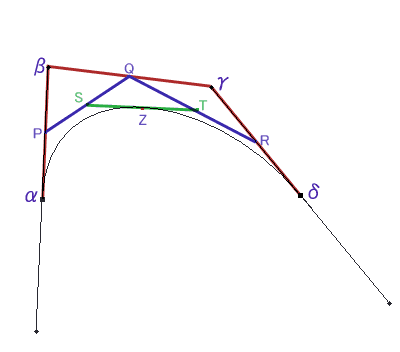 図4:ベクトルライン「Z」との交点 線分α−βとの中点を「P」 β−γとの中点を「Q」 γ−δとの中点を「R」とし、線分P−QとQ−Rを作成します。そして、この二つの線分の中点をそれぞれ「S」「T」とし、この線分S−Tとの中点をを「Z」とおきます。 すべての線と点をそれぞれの中点で結ぶと、その点Zは、パスライン「α−δ」との接点にあたります。 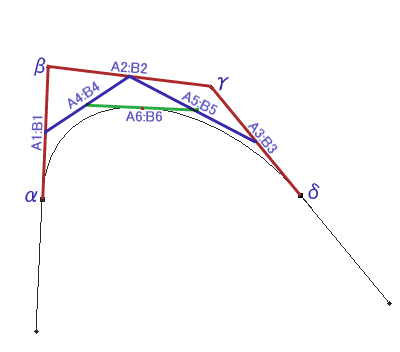 図5:座標の各点の名称 今回は、 A1:B1 = A2:B2 = A3:B3 = A4:B4 = A5:B5 = A6:B6 = 1:1の対比を例にしてラインを描いてみましたが、これらそれぞれの対比を同列にした場合、かならずその点Zは パスラインα−δ上に存在します。 A1:B1 = A2:B2 = A3:B3 = A4:B4 = A5:B5 = A6:B6 = 1:2 A1:B1 = A2:B2 = A3:B3 = A4:B4 = A5:B5 = A6:B6 = 3:2 など 一般に、各線分をm:nの比で分割した点Zはパスライン「αーδ」上の点となります つまりは、パスラインα−δは、0:1 〜 1:0 までの連続した点を上記の式で導き出し、その連続点を結んだラインということになります。 ですから、凸型多角形で生成されたパスラインは、この多角形の外に出ることはありえないわけです。 結局書きたかったことはこれなのですが、随分と前ふりが長くなってしまいました。 4:パスの性質 (中・上級編) では、Photoshopにおけるパスのラインの考え方はどうでしょう。 実は基本的な部分は上記「3」の計算式と全く同一のものです。 ただ、アンカーポイントが複数存在しますから、各点から伸びる方向ベクトル情報も、二種類になります。 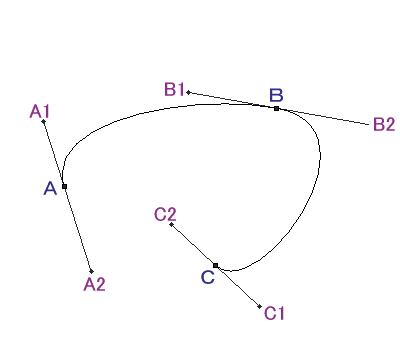 図6:各点のパスに及ぼす影響 例えば図6のようなパスのラインの場合、パス線分をA−B と B−Cの2つに分けることが出来ます。 A−Bのラインに影響を及ぼす方向ベクトル情報は「A1」「B1」の2つです。 これは上記でも示したとおりです。 つまり、それら以外の方向ベクトル情報(A2、B2、C1、C2)は、パスラインA−Bには干渉しないのです。干渉しないのですから、これらの点がどのようなベクトルであろうとも、パスラインA−Bには一切影響を及ぼしません。 同様に、パスラインB−Cでは、「B2」「C1」がベクトル生成時の情報として扱われ、それら以外の情報には干渉されません。 これが、アンカーポイントから方向ベクトルが2本派生している理由です。 では、どうして個別のはずのこれらのベクトルラインが一本の線として綺麗なラインを描けるのでしょうか。これもまた理由は簡単で、それぞれのアンカーポイントから出ている2本の方向ベクトル(Ex:A1とA2等)が、アンカーポイントを中心としている一本の線であるからです。 例えば、点Bを見てください。 この点は、パスラインA−BとB−Cの橋渡しをしている中間地点ですが、点Bと直線「B1−B2」が完璧に水平で交わっています。 ちょっと分かりにくい表現ですが、ようは、直線「B1−B2」の外側(図6では上方向ですね)へパスラインA−B−Cがはみ出していないということです。これは、水平上に球体を置いているのと同じで、点Bは、あくまでパスラインA−Cを描く上での通過点でしかないことを示しています。 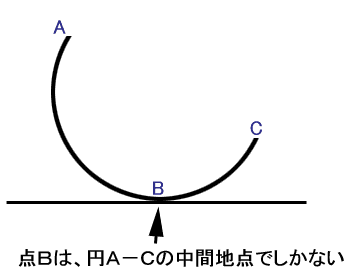 図7:複数点のベクトルが綺麗なラインを描く理由 5:オープンパスとクローズパス しつこいですが、パスには点Aと点Bの方向ベクトルを算出してラインを描きますから、先ほどのパスでは始点と終点のベクトル情報は無駄になります。 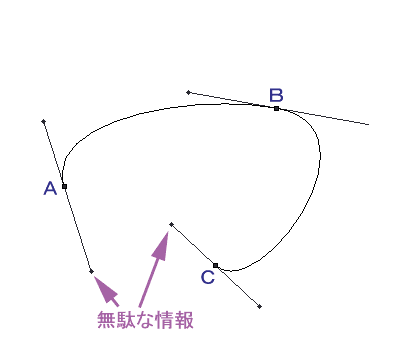 図8:無駄なベクトル情報 パスにはオープンパスとクローズパスの2種類があり、 図8まで使用してきたパスの例はすべてオープンパスに属します。 ようは、パスに始点と終点があり、そこにオープンの部分があるからですが、こういったパスは当然、始点と終点は、情報をもってはいますが、無駄になります。 これに対して、クローズパスは、始点と終点(図8でいうA点とC点)がもつ二つの無駄な方向ベクトル情報を元にしてひとつの円として描いたもので、すべてのアンカーポイントから出るすべての方向ベクトル情報を利用したものであるといえます。 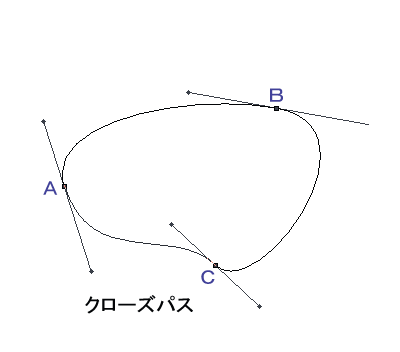 図9:A点とC点を結んだクローズパス クローズパス、オープンパスどちらが良いということはありません。 適材適所で臨機応変に使い分けていけばよいですが、例えばメカでパーツを描く場合、そのパーツは物体である以上、始点と終点があることは物理的にありえません。 ですからパーツの外枠部はクローズパス、中の装飾は必要に応じてオープンパスで描く習慣をつけることをお勧めします。  図10:パスを用いて作図した例 この綺麗なラインを持った図形は、フリーハンドでは絶対に描けません。 メカニカルな、ラインの均整の取れた美しい画像は、パスを用いることによって簡単にすばやく描くことが出来るのです。 キャプチャした画像は Adobe Photoshop4.01 のものです |